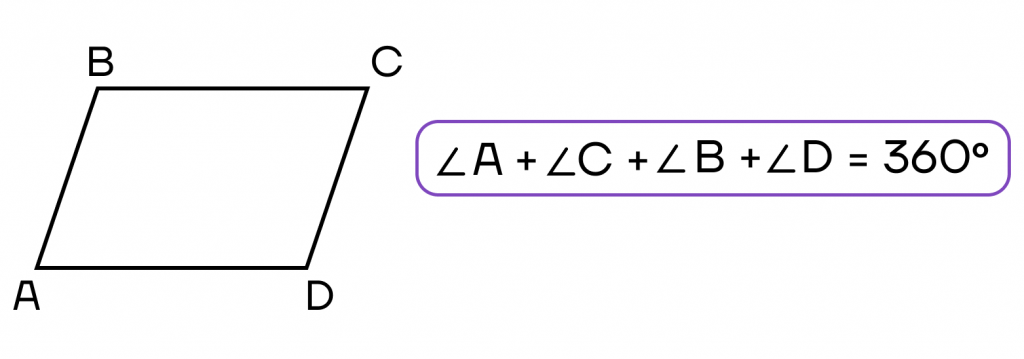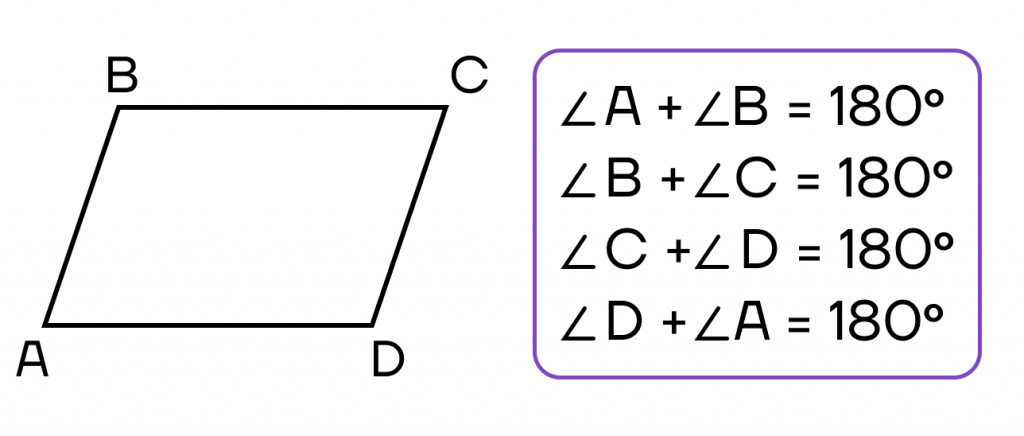- Параллелограмм. Формулы, признаки и свойства параллелограмма
- Признаки параллелограмма
- Основные свойства параллелограмма
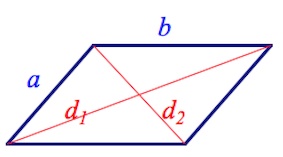
- Стороны параллелограмма
- Формулы определения длин сторон параллелограмма:
- Диагонали параллелограмма
- Формулы определения длины диагонали параллелограмма:
- Периметр параллелограмма
- Формулы определения длины периметра параллелограмма:
- Площадь параллелограмма
- Формулы определения площади параллелограмма:
- Параллелограмм. Свойства и признаки параллелограмма
- Определение параллелограмма
- Свойства параллелограмма
- Признаки параллелограмма
- Параллелограмм
- На этой странице вы узнаете
- Параллелограмма
- Признаки параллелограмма
- Свойства параллелограмма
- Биссектриса в параллелограмме
- Площадь параллелограмма
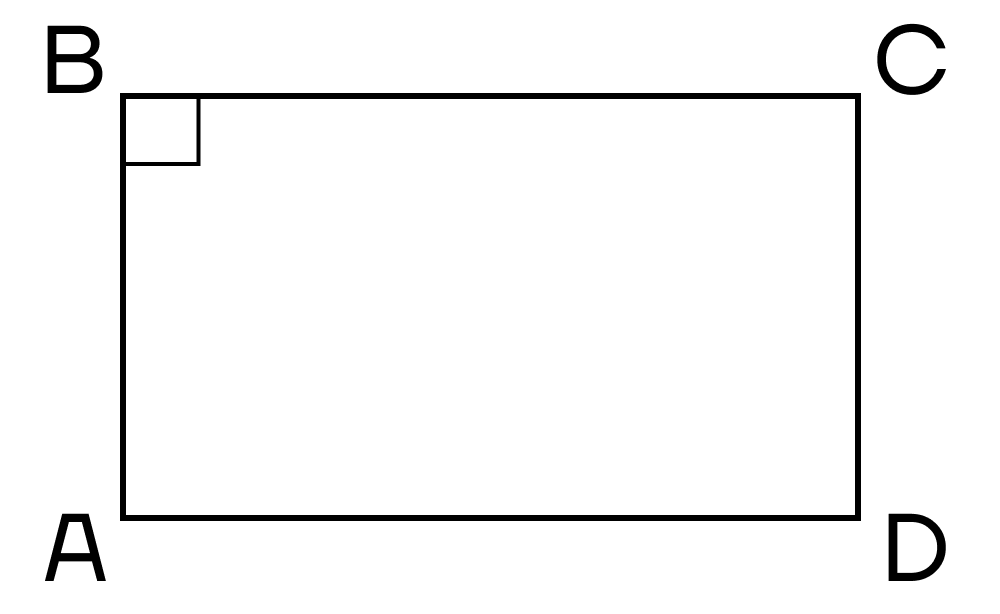
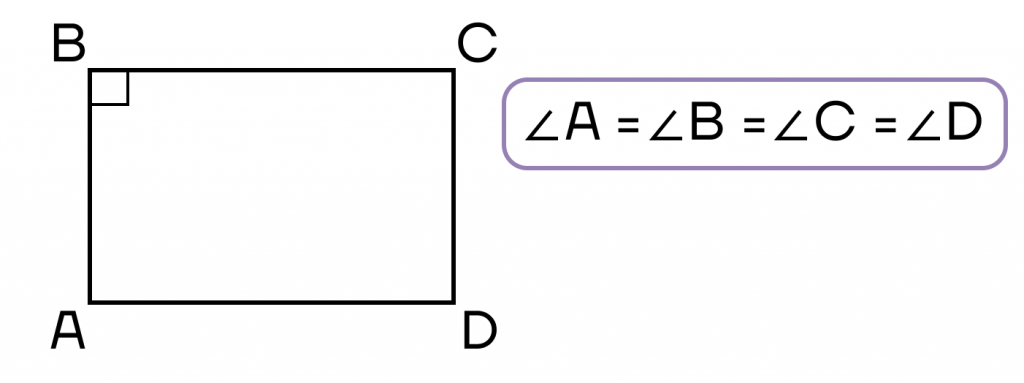
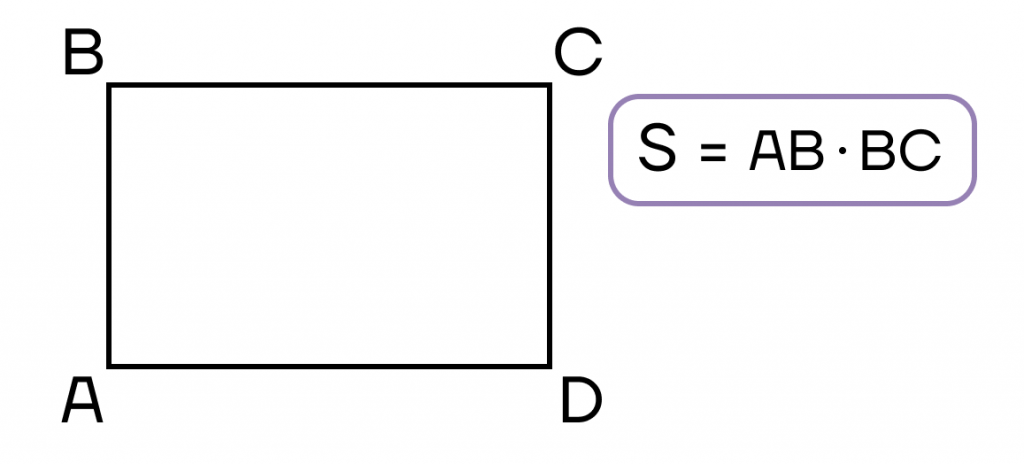
- Прямоугольник
- Признаки прямоугольника
- Свойства прямоугольника
- Биссектриса и площадь прямоугольника
- Ромб
- Всё о ромбе
- Квадрат
- Всё о квадрате
- Фактчек
- Проверь себя
Параллелограмм. Формулы, признаки и свойства параллелограмма
 | 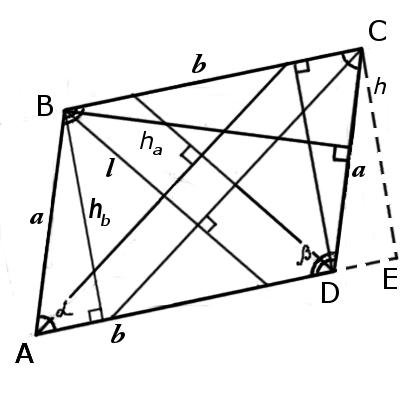 |
| Рис.1 | Рис.2 |
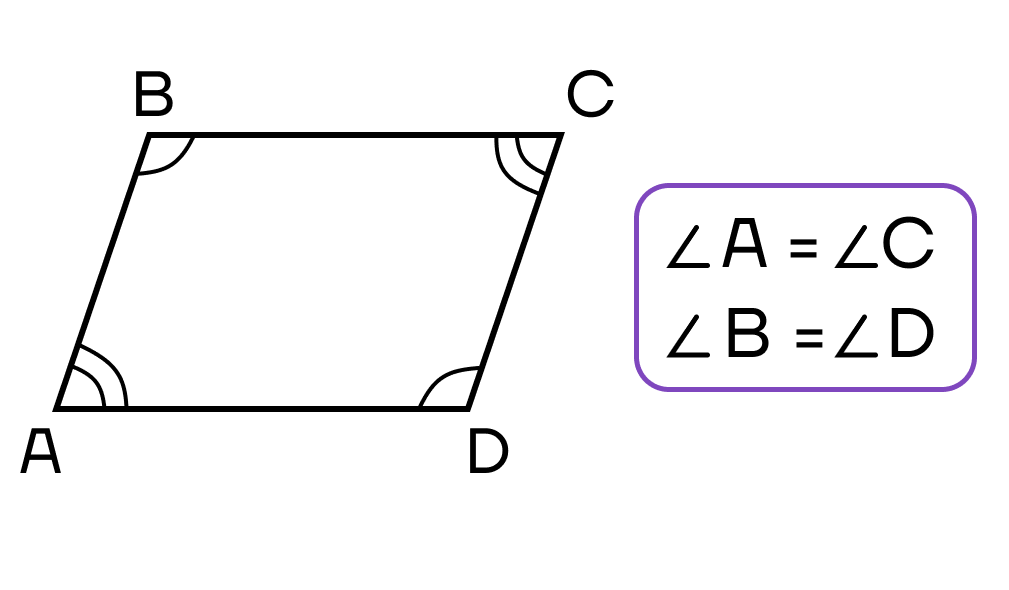
Признаки параллелограмма
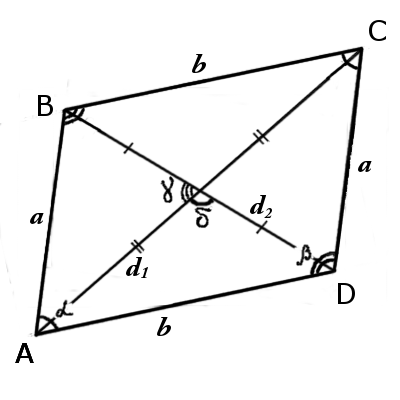
AB||CD, AB = CD (или BC||AD, BC = AD)
∠DAB = ∠BCD, ∠ABC = ∠CDA
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
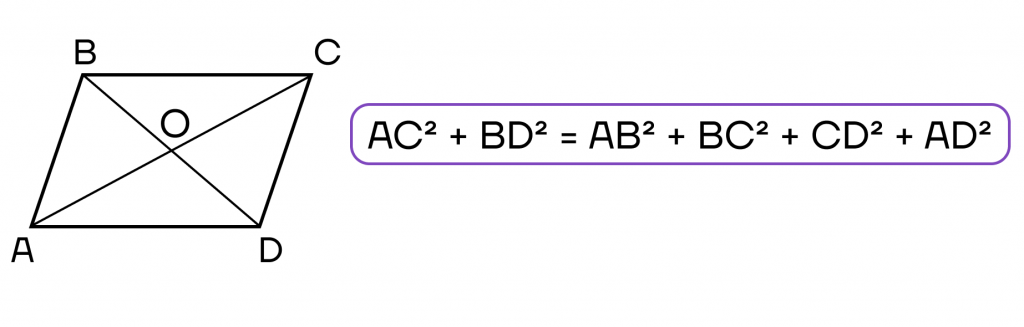
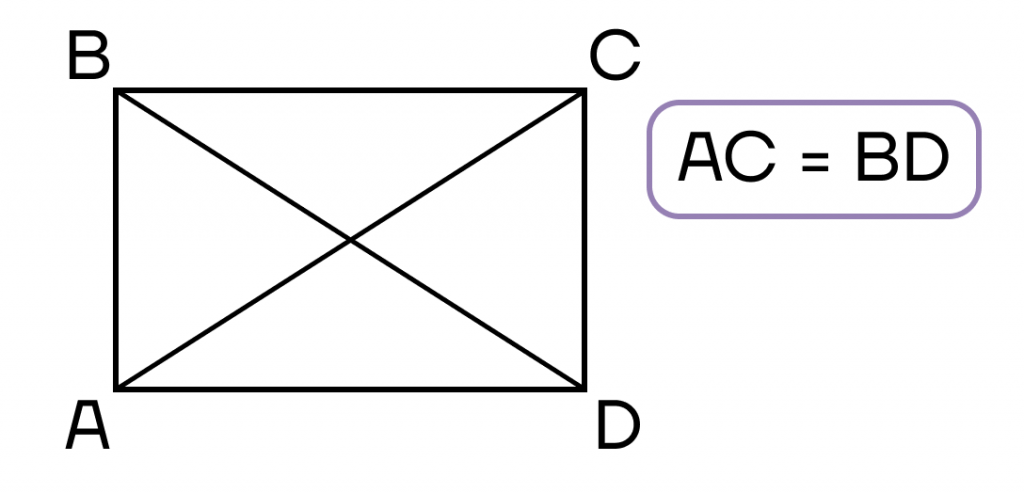
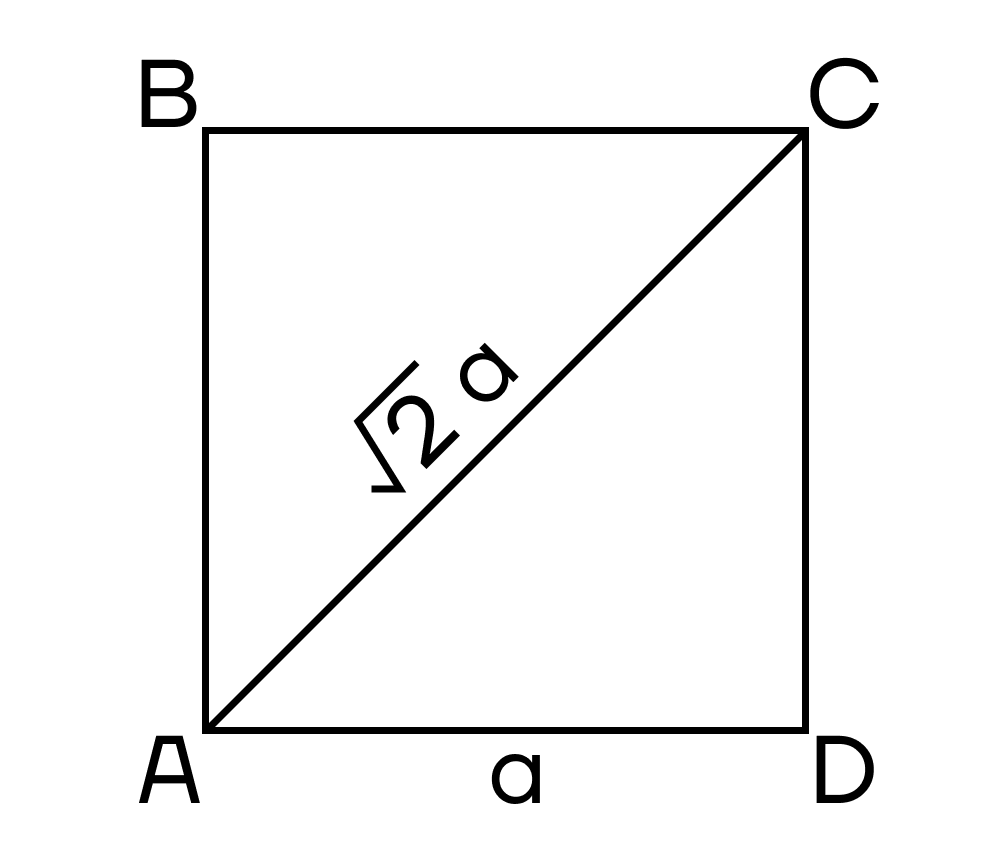
AC 2 + BD 2 = AB 2 + BC 2 + CD 2 + AD 2
Основные свойства параллелограмма
∠ABC = ∠CDA, ∠BCD = ∠DAB
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
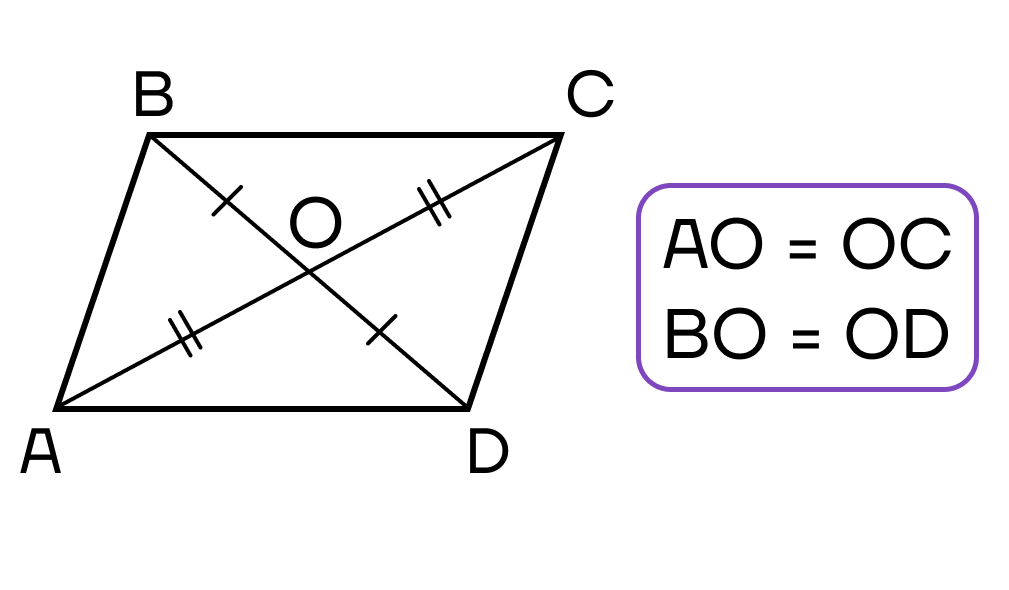
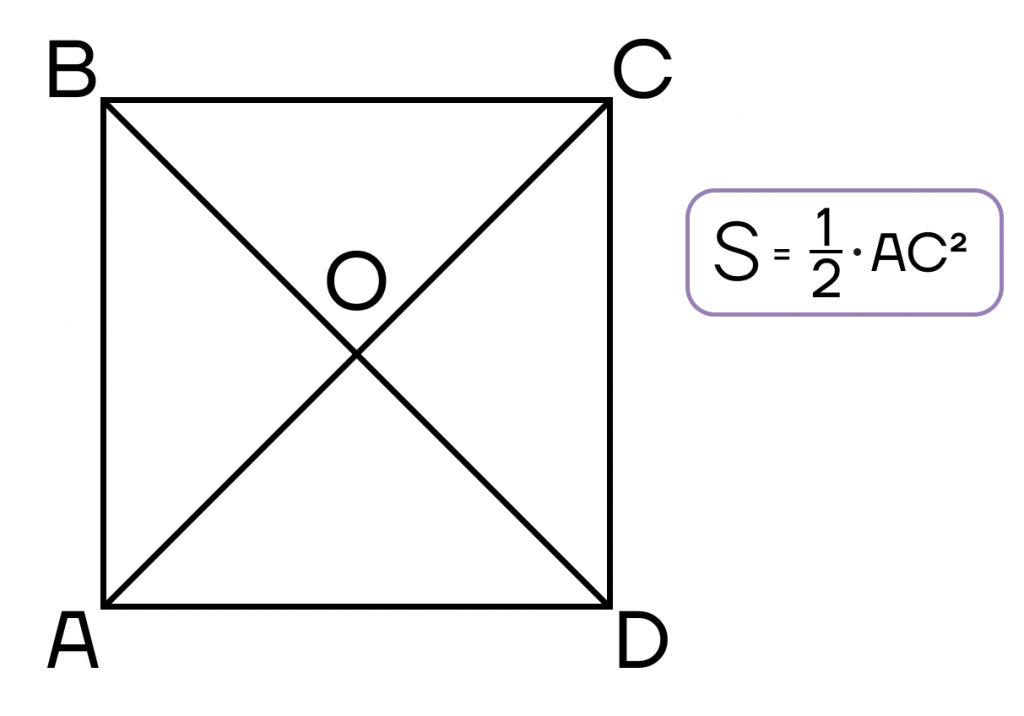
8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам:
| AO = CO = | d 1 |
| 2 | |
| BO = DO = | d 2 |
| 2 |
AC 2 + BD 2 = 2AB 2 + 2BC 2
Стороны параллелограмма
Формулы определения длин сторон параллелограмма:
1. Формула сторон параллелограмма через диагонали и угол между ними:
2. Формула сторон параллелограмма через диагонали и другую сторону:
| a = | √ 2 d 1 2 + 2 d 2 2 — 4 b 2 |
| 2 |
| b = | √ 2 d 1 2 + 2 d 2 2 — 4 a 2 |
| 2 |
3. Формула сторон параллелограмма через высоту и синус угла:
| a = | h b |
| sin α |
| b = | h a |
| sin α |
4. Формула сторон параллелограмма через площадь и высоту:
| a = | S |
| ha |
| b = | S |
| hb |
Диагонали параллелограмма
Формулы определения длины диагонали параллелограмма:
d 1 = √ a 2 + b 2 — 2 ab·cosβ
d 2 = √ a 2 + b 2 + 2 ab·cosβ
d 1 = √ a 2 + b 2 + 2 ab·cosα
d 2 = √ a 2 + b 2 — 2 ab·cosα
d 1 = √ 2 a 2 + 2 b 2 — d 2 2
d 2 = √ 2 a 2 + 2 b 2 — d 1 2
4. Формула диагонали параллелограмма через площадь, известную диагональ и угол между диагоналями:
| d 1 = | 2S | = | 2S |
| d 2· sinγ | d 2· sinδ |
| d 2 = | 2S | = | 2S |
| d 1· sinγ | d 1· sinδ |
Периметр параллелограмма
Формулы определения длины периметра параллелограмма:
P = 2 a + 2 b = 2( a + b )
P = 2 a + √ 2 d 1 2 + 2 d 2 2 — 4 a 2
P = 2 b + √ 2 d 1 2 + 2 d 2 2 — 4 b 2
3. Формула периметра параллелограмма через одну сторону, высоту и синус угла:
| P = | 2( b + | h b | ) |
| sin α |
| P = | 2( a + | h a | ) |
| sin α |
Площадь параллелограмма
Формулы определения площади параллелограмма:
3. Формула площади параллелограмма через две диагонали и синус угла между ними:
| S = | 1 | d 1 d 2 sin γ |
| 2 |
| S = | 1 | d 1 d 2 sin δ |
| 2 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Источник
Параллелограмм. Свойства и признаки параллелограмма
Определение параллелограмма
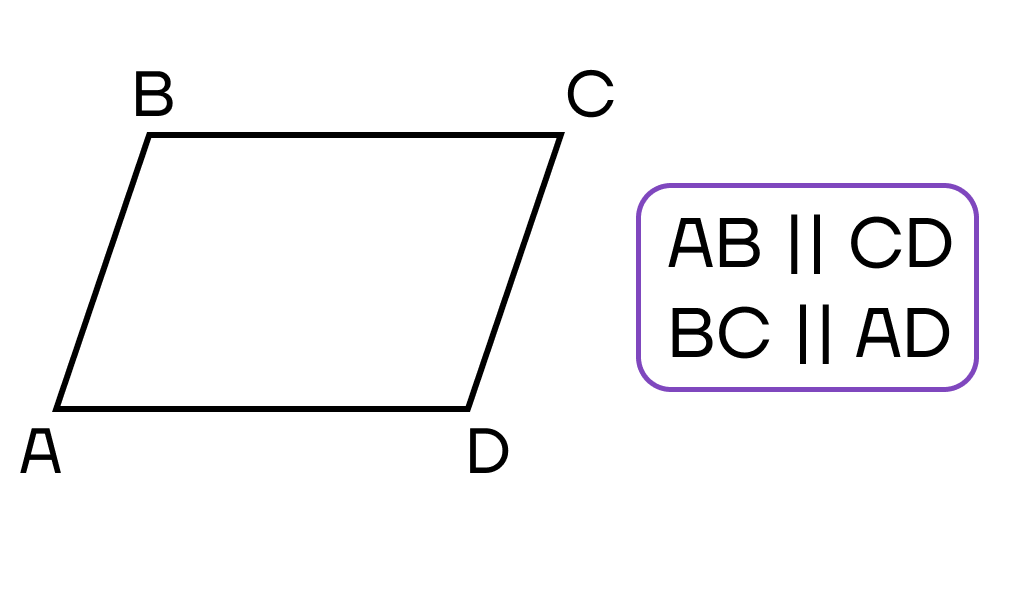
Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.
Свойства параллелограмма
1. Противоположные стороны параллелограмма попарно равны
2. Противоположные углы параллелограмма попарно равны
3. Сумма смежных (соседних) углов параллелограмма равна 180 градусов
4. Сумма всех углов равна 360°
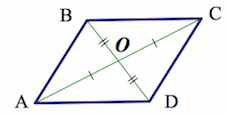
6. Точка пересечения диагоналей является центром симметрии параллелограмма
7. Диагонали параллелограмма и стороны
связаны следующим соотношением:
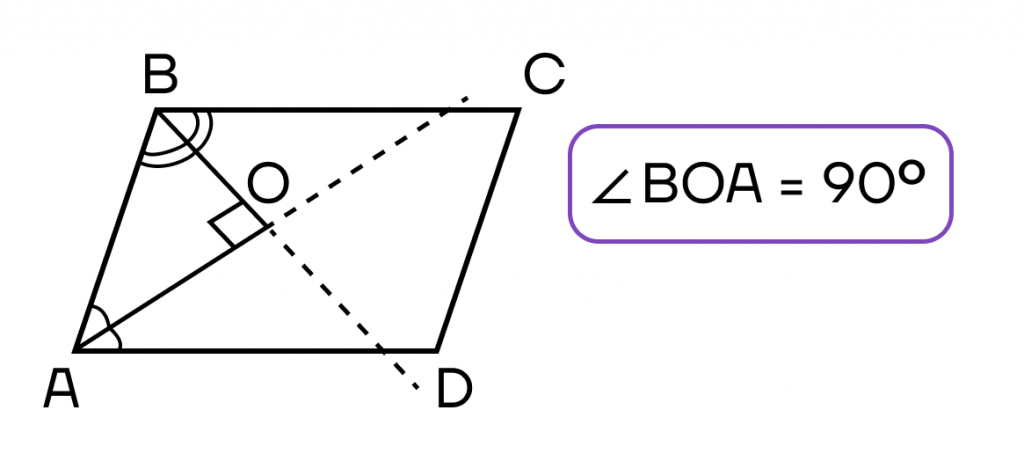
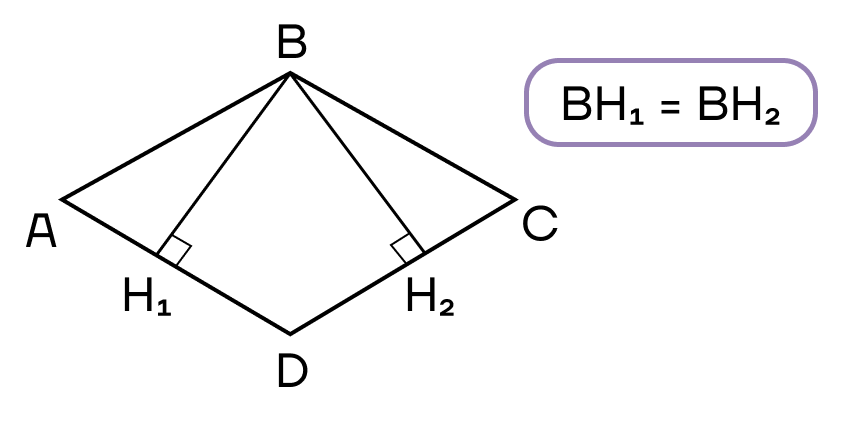
8. Биссектриса отсекает от параллелограмма равнобедренный треугольник
Признаки параллелограмма
Четырехугольник является параллелограммом, если выполняется хотя бы одно из следующих условий:
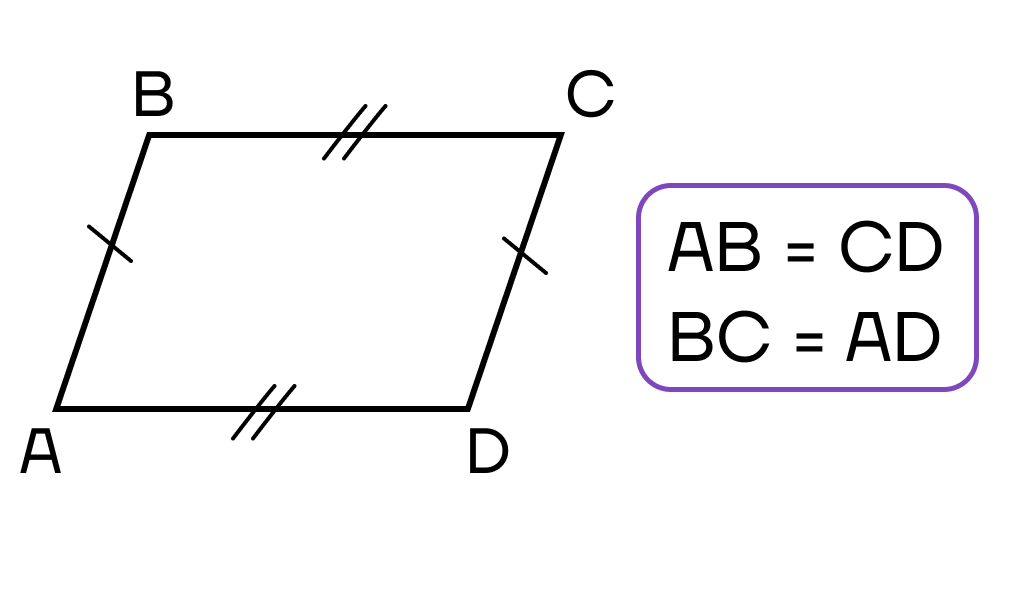
1. Противоположные стороны попарно равны:
2. Противоположные углы попарно равны:
3. Диагонали пересекаются и в точке пересечения делятся пополам
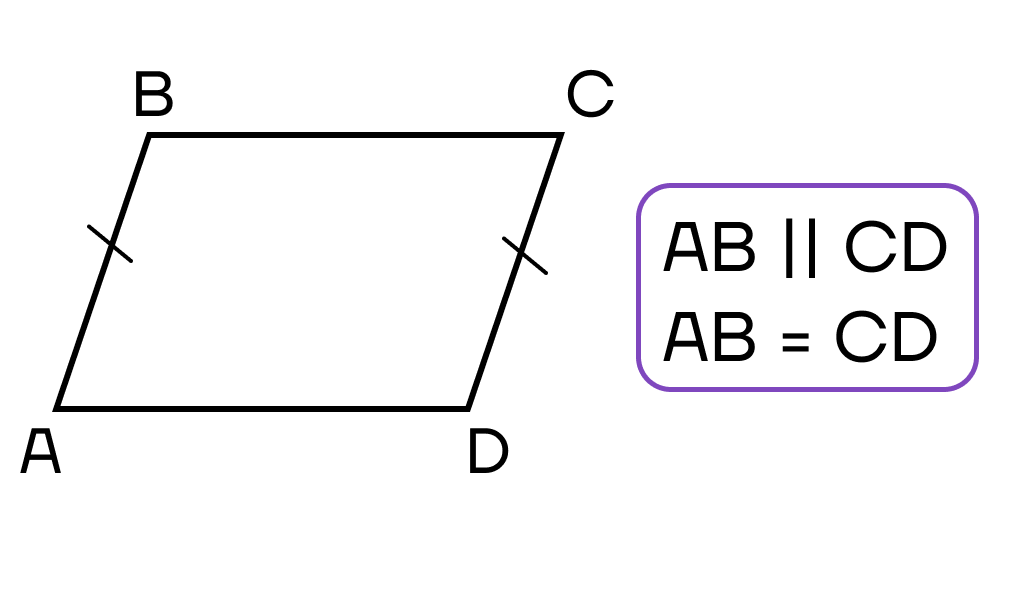
4. Противоположные стороны равны и параллельны:
5.
Небольшой видеоролик о свойствах параллелограмма (в том числе ромба, прямоугольника, квадрата) и о том, как эти свойства применяются в задачах:

Хорошую подборку задач на нахождение углов и длин в параллелограмме смотрите здесь.
Источник
Параллелограмм
На этой странице вы узнаете
- Чем отличаются признаки от свойств?
- Сколько крыс у биссектрисы?
- Гибридом чего будет квадрат?
Когда мы видим изображение с множеством деталей, наш мозг автоматически раскладывает их на простые фигуры. Этот процесс занимает доли секунды. Разные геометрические фигуры вызывают у нас разные ощущения, эмоции и ассоциации.А что будет, если мы задержим взгляд на одной из них и разберем подробнее? Давайте сделаем так с параллелограммом.
Параллелограмма
Параллелограмм – это четырёхугольник, чьи стороны попарно параллельны и равны.
Параллелограмм мы видим достаточно часто.
Признаки параллелограмма
У параллелограмма есть три основных признака. Если для четырехугольника выполняется хотя бы один из признаков, такой четырехугольник можно называть параллелограммом.
Признаки параллелограмма:
- Две противоположные стороны четырехугольника параллельны и равны.
- Противоположные стороны четырехугольника попарно равны.
- Диагонали четырехугольника пересекаются и в точке пересечения делятся пополам.
Свойства параллелограмма
| Чем отличаются признаки от свойств? |
Свойства нельзя путать с признаками, хоть они и очень похожи. Свойствами параллелограмма обладает фигура, уже являющаяся параллелограммом, тогда как признаки предназначены для выявления параллелограммов среди четырехугольников.
Свойства параллелограмма:
- Противолежащие стороны равны.
- Противолежащие стороны параллельны.
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Сумма углов, прилежащих к любой стороне, равна 180 0 .
- Сумма квадратов диагоналей равна сумме квадратов всех сторон.
- Диагонали делят параллелограмм на четыре треугольника с одинаковой площадью.
- Каждая диагональ делит параллелограмм на два равных треугольника
Биссектриса в параллелограмме
Можно ли провести биссектрису в параллелограмме? Да. Биссектриса параллелограмма – это луч, исходящий из вершины угла параллелограмма, делящий этот угол на два равных угла и пересекающий одну из сторон параллелограмма.
| Сколько крыс у биссектрисы? |
Значение биссектрисы легко запомнить, используя фразу “Биссектриса – это крыса, она бегает по углам и делит угол пополам”.
Так как у треугольника три угла – соответственно, и крыс-биссектрис тоже три.
Два факта связанные с биссектрисой в параллелограмме:
- Биссектриса, проведенная из угла параллелограмма, отсекает от него равнобедренный треугольник.
- Биссектрисы углов, принадлежащих одной стороне параллелограмма, пересекаются под прямым углом.
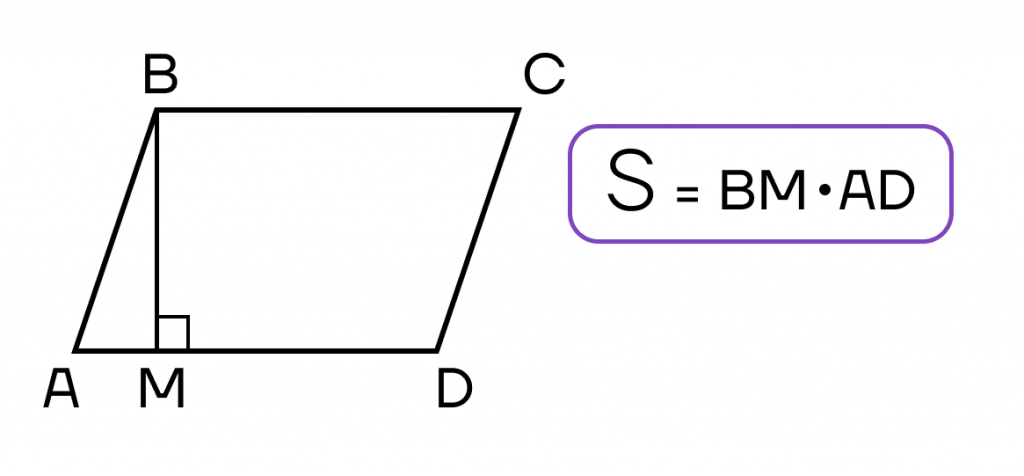
Площадь параллелограмма
Есть три формулы площади параллелограмма, которые применяются в зависимости от известных величин
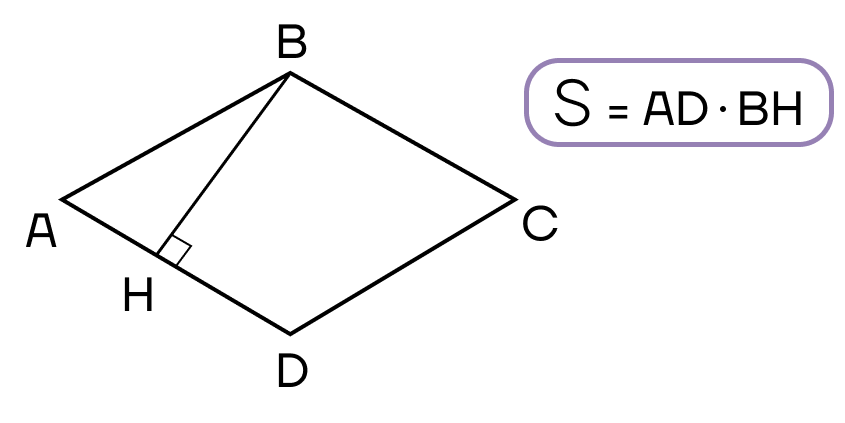
- Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
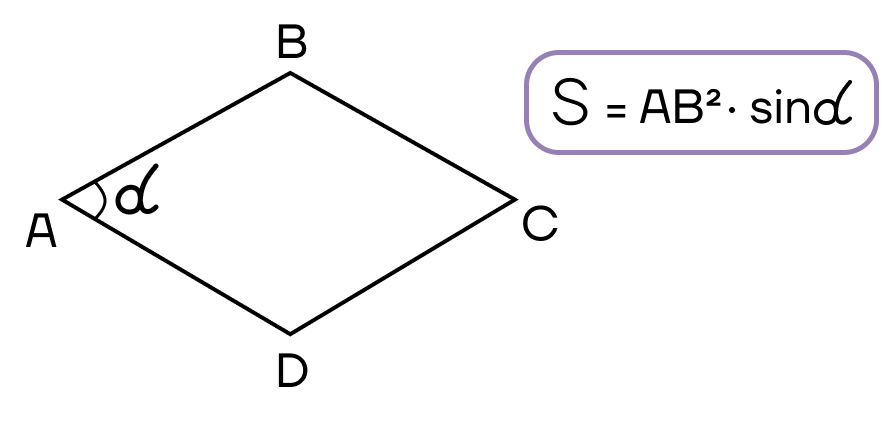
- Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними.
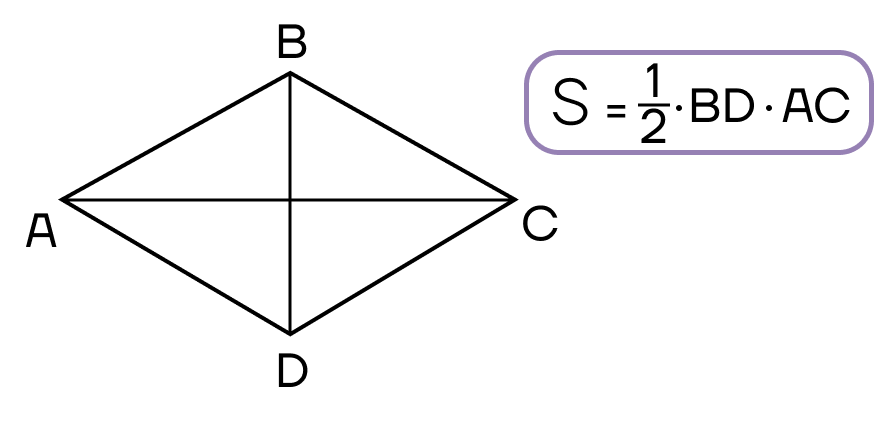
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними.
Прямоугольник
Как параллелограмм связан с прямоугольником?
Прямоугольник – это параллелограмм, углы которого по 900.
Данную фигуру часто называют частным случаем параллелограмма. Из этого следует, что для прямоугольника применимы те же признаки и свойства, что для параллелограмма, но и имеется ряд собственных.
В жизни прямоугольником можно назвать дверь, картину или фотографию:
Признаки прямоугольника
- Параллелограмм, имеющий хотя бы один прямой угол.
- Параллелограмм, все углы которого равны.
- Параллелограмм, диагонали которого равны.
- Четырехугольник, у которого три прямых угла.
Свойства прямоугольника
- Стороны прямоугольника одновременно являются и его высотами.
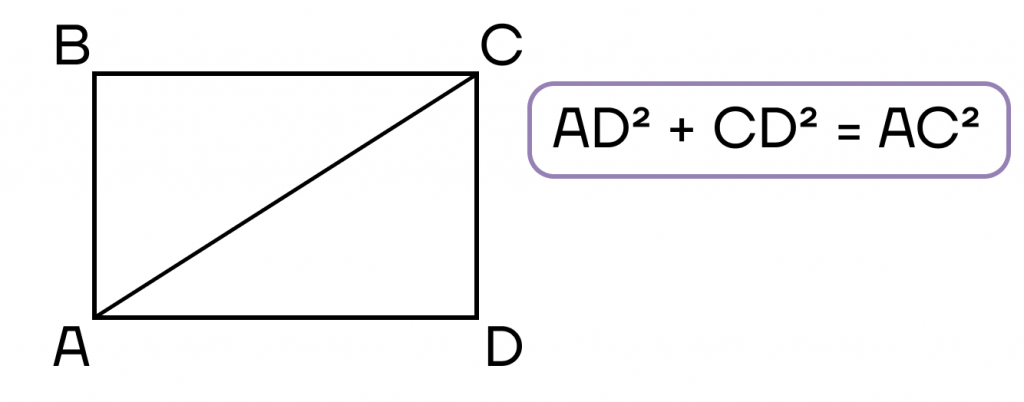
- Сумма квадратов двух прилежащих сторон равна квадрату диагонали.
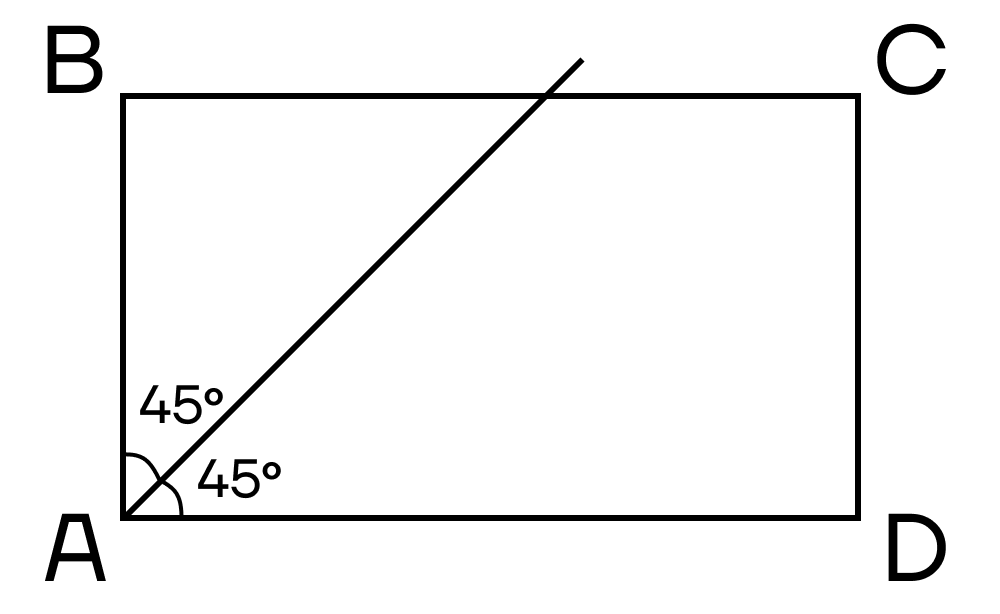
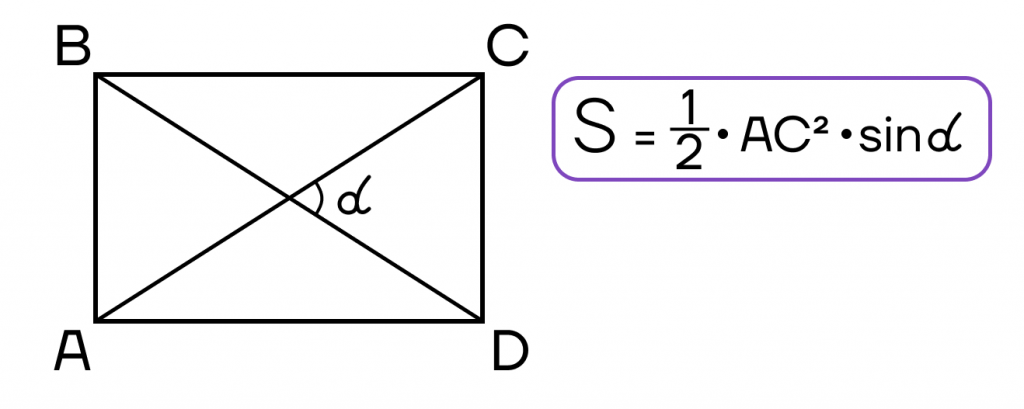
Биссектриса и площадь прямоугольника
Биссектриса делит угол прямоугольника на два угла по 45 0 и пересекает одну из сторон прямоугольника.
Теперь рассмотрим два способа нахождения площади прямоугольника:
- Площадь прямоугольника равна произведению двух соседних сторон.
- Площадь прямоугольника равна половине произведения квадрата диагонали на синус угла между диагоналями.
Ромб
Пожалуй, это самая неустойчивая фигура.
Ромб – это параллелограмм, у которого все стороны равны.
Ромб можно увидеть на знаке машины “Митсубиси”, их там целых три.
А также в игровых наградах:
Также является частным случаем параллелограмма и обладает его признаками и свойствами, но имеет и собственные.
Всё о ромбе
Признаки ромба:
- Две смежные стороны параллелограмма равны.
- Диагонали параллелограмма пересекаются под прямым углом.
- Диагональ параллелограмма делит каждый угол пополам.
- Четырехугольник, у которого все стороны равны.
Свойства ромба:
- Диагонали пересекаются под прямым углом и точкой пересечения делятся пополам.
- Диагонали являются биссектрисами.
Как уже отмечено в свойствах ромба, биссектрисой ромба является диагональ.
Как найти площадь ромба?
Для нахождения площади ромба есть три разные формулы:
- Площадь ромба равна произведению стороны и высоты ромба.
- Площадь ромба равна половине произведения его диагоналей.
- Площадь ромба равна произведению квадрата стороны на синус угла ромба.
Квадрат
А вот квадрат, наоборот, достаточно устойчив.
Квадрат – это четырехугольник, у которого все углы и стороны равны.
| Гибридом чего будет квадрат? Если внимательно посмотреть на определение, то можно заметить, что квадрат объединяет в себе и параллелограмм, и прямоугольник, и ромб. |
Квадратом может быть крышка подарочной коробки или окно.
Рассмотрим признаки и свойства данной фигуры.
Всё о квадрате
Признаки квадрата:
- Ромб, у которого хотя бы один угол прямой.
- Ромб, у которого все углы равны.
- Ромб, у которого диагонали равны.
- Четырехугольник, диагонали которого равны и перпендикулярны.
Свойства квадрата:
- Диагональ квадрата равна 2 стороны квадрата.
- Диагонали делят квадрат на четыре равных треугольника.
Биссектрисой квадрата, как и у ромба, является диагональ.
Рассмотрим формулы для нахождения площади квадрата:
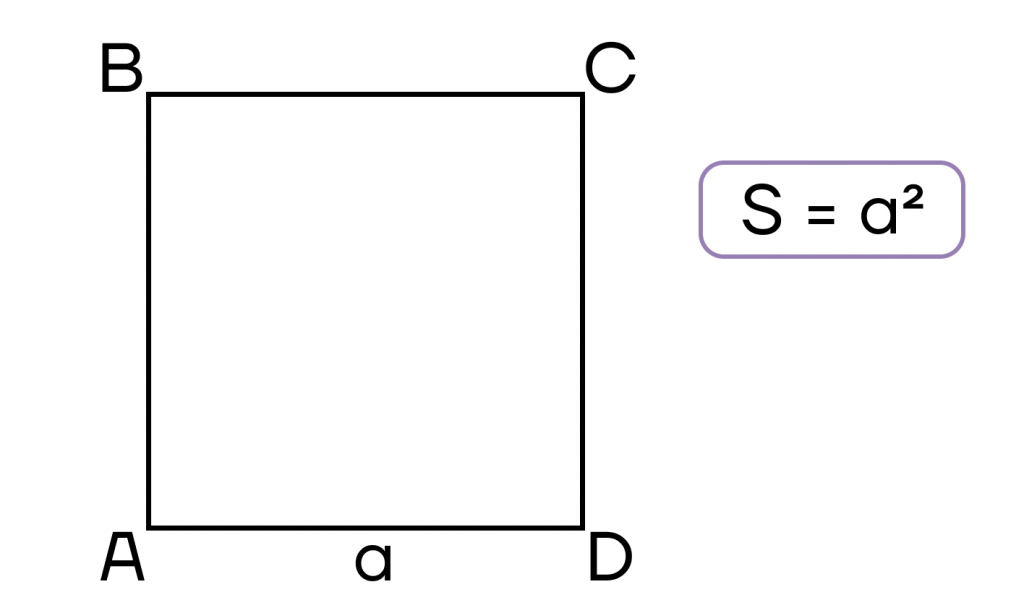
- Площадь квадрата равна квадрату его стороны.
- Площадь квадрата равна половине квадрата диагонали.
Фактчек
- Параллелограмм – это четырёхугольник, чьи стороны попарно параллельны и равны.
- Прямоугольник – это параллелограмм, углы которого по 900 и диагонали которого равны.
- Ромб – это параллелограмм, у которого все стороны равны, а также диагонали перпендикулярны друг другу
- Квадрат – это четырехугольник, у которого все углы и стороны равны. Квадрат является гибридом параллелограмма, прямоугольника и ромба.
Проверь себя
Задание 1.
Найдите площадь параллелограмма, если его стороны 5 и 8, а угол между ними 30 0
Задание 2.
Найдите площадь прямоугольника, если его диагональ 12, а угол между диагоналями 60 0
Задание 3.
Найдите площадь ромба, если его диагонали 6 и 10
Задание 4.
У четырехугольника диагонали пересекаются под углом 30 0 , а его стороны попарно параллельны и равны. Что это за фигура?
Задание 5.
У четырехугольника две противоположные стороны параллельны и равны и есть один прямой угол. Что это за фигура?
Ответы: 1. – 2; 2. – 3; 3. – 1; 4. – 4; 5. – 3
Источник