- Вычислить площадь правильного шестиугольника онлайн
- Через длину стороны
- Через периметр
- Через длинную диагональ
- Через короткую диагональ
- Через радиус описанной окружности
- Через радиус вписанной окружности
- Что такое правильный шестиугольник
- Гексагон
- Свойства правильного шестиугольника
- Калькулятор периметра шестиугольника
- Геометрия шестиугольника
- Примеры шестиугольников
- Периметр гексагона
- Примеры из реальной жизни
- Снежинка
- Школьная задача
- Заключение
- Шестиугольник описанный около окружности формулы
- Через сторону
- Через радиус описанной окружности
Вычислить площадь правильного шестиугольника онлайн
Шестиугольник — многоугольник, у которого есть шесть сторон и шесть углов. В правильном заданном многоугольном геометрическом объекте все стороны равняются друг другу, а углы формируют шесть равносторонних треугольников.
Площадь правильной фигуры с шестью углами — положительная величина некоторой области плоскости, занимаемой данным многоугольным геометрическим объектом.
Выделяют ряд методов нахождения площади этого многоугольника, зависимо от его типа.
Через длину стороны
По той причине, что выпуклый шестиугольник включает в себя шесть равносторонних треугольников, тогда формула нахождения требуемой величины через длину стороны выглядит следующим образом:
где a — это продолжительность стороны.
Всё достаточно просто, если сторона заранее известна. Если же эта величина нам не дана, но известен периметр или апофема — высота одного из шести равносторонних треугольников — тогда длину стороны можно высчитать.
В случае, если известен периметр, его необходимо поделить на шесть, таким образом получается длина стороны. К примеру, если периметр равен 36, то, поделив 36 на 6, получается 6 — это и есть протяжённость стороны.
Если известна лишь апофема, тогда можно посчитать длину стороны, подставив апофему в формулу b = x√3 и умножив ответ на 2. Всё это потому, что апофема — это сторона x√3 составляемого ей треугольника с углами 30, 60 и 90 градусов. К примеру, если апофема 11√3, то x = 11, а протяжённость стороны будет эквивалентна 22.
Через периметр
Если при изучении правильной фигуры с шестью углами нам известен только его периметр, несложно рассчитать площадь этой фигуры по такой формуле:
где p — это периметр фигуры.
Допустим, если периметр будет равняться 24, тогда площадь будет примерно эквивалентна 42. Если в качестве периметра возьмём число 50, тогда площадь фигуры окажется 180.
Через длинную диагональ
Длинная или большая диагональ шестиугольника — это диаметр описанной вокруг него плоской кривой, как правило, она равняется двум его сторонам.
Используем такое выражение для подсчёта площади подобного правильного многоугольного геометрического объекта через длинную диагональ этого множества точек:
где D — это длинный отрезок, соединяющий несмежные вершины.
К примеру, если D = 6, тогда заданная характеристика замкнутого выпуклого многоугольника будет приблизительно равна 23. Если в качестве длинной диагонали возьмём 8, тогда величина будет примерно эквивалентна 42.
Через короткую диагональ
Меньшая или короткая диагональ правильного шестиугольника в √3 раз длиннее его стороны, также она образует с ней прямой угол.
Если известна короткая диагональ такого выпуклого многоугольника, то с её помощью можно найти площадь этой фигуры следующим образом:
где D — это протяжённость короткого отрезка, соединяющего несмежные вершины.
К примеру, если длина такой диагонали будет равна 14, тогда необходимая характеристика фигуры будет примерно равняться 170. Если же в качестве D мы возьмём 2, тогда величина окажется всего лишь 3.
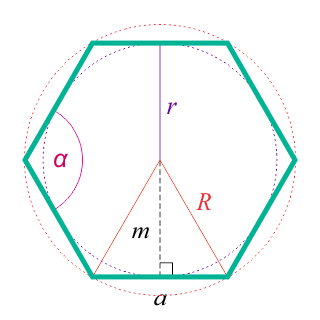
Через радиус описанной окружности
Шестиугольник считается правильным многоугольником, ведь все его стороны и углы эквивалентны друг другу. Соответственно, около такого многоугольника можно описать окружность.
Чтобы найти площадь выпуклого многоугольника через радиус описанной окружности, необходимо воспользоваться такой формулой:
где R — это отрезок, соединяющий центр и любую точку описанной замкнутой плоской кривой.
К примеру, если отрезок, соединяющий центр и любую точку, равняется 5, тогда заданная характеристика замкнутой фигуры будет примерно равна 65. Если же в качестве радиуса возьмём число 12, соответственно, заданная характеристика замкнутой фигуры получится примерно 374.
Через радиус вписанной окружности
Шестиугольник считается правильным многоугольником, ведь все его стороны и углы равны друг другу. Соответственно, во всякий шестиугольник можно вписать окружность.
Формула для расчёта площади следующего выпуклой фигуры с шестью углами через радиус вписанной окружности будет выглядеть следующим образом:
где r — это отрезок, соединяющий центр и любую точку вписанной замкнутой плоской кривой.
К примеру, если этот отрезок, соединяющий центр и любую точку, равен 14, тогда необходимая величина этого множества точек будет примерно равна 679. Если в качестве отрезка, соединяющего центр и любую точку, возьмем 4, тогда площадь будет приблизительно равна 55.
Что такое правильный шестиугольник
Этот многоугольный геометрический объект имеет определённые свойства:
- Каждый угол этой фигуры равняется 120 градусам;
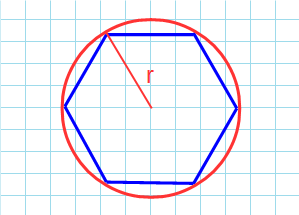
- Вокруг правильного шестиугольника можно описать окружность, причем единственную, а её радиус равняется его стороне;
- Большие диагонали такого выпуклого многоугольника разделяют его на шесть равносторонних треугольников, высота каждого равняется радиусу вписанной в выпуклый многоугольник окружности;
- Центры вписанной и описанной окружностей около подобного выпуклого многоугольника — это точка пересечения больших диагоналей этого множества точек.
Эта фигура очень часто встречается в природе, технике и культуре. К примеру:
- Пчелиные соты изображают разделение плоскости на выпуклые шестиугольники;
- Некоторые сложные молекулы углерода имеют гексагональную кристаллическую решётку;
- Сечение гайки и большинства карандашей описывается таким выпуклым многоугольником;
- Гексаграмма — это шестиконечная звезда, сформированная двумя правильными треугольниками. Также её называют звездой Давида, она считается символом иудаизма.
Источник
Гексагон
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
Шестиугольник — это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.
Выпуклый шестиугольник — это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Правильный шестиугольник — это шестиугольник, все стороны которого равны между собой.
Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 — 2 ) = 720 градусов.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Свойства правильного шестиугольника
- все внутренние углы равны между собой
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
- сторона правильного шестиугольника равна радиусу описанной окружности
- большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
- меньшая диагональ правильного шестиугольника в раз больше его стороны.
- vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
- правильный шестиугольник заполняет плоскость без пробелов и наложений
- диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
- инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
- nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60° .
Внутренние углы Внутренние углы в правильном шестиугольнике равны :
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
Радиус описанной окружности равен стороне правильного шестиугольника:
Периметр правильного шестиугольника
Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
,
где − полупериметр шестиугольника.
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Источник
Калькулятор периметра шестиугольника
Правильный шестиугольник или гексагон — это многоугольник с шестью равными углами и шестью равными сторонами. Это правильная фигура, которая широко встречается как в природе, так и в человеческой повседневности.
Геометрия шестиугольника
Шестиугольник — фигура на плоскости, ограниченная шестью равными отрезками, которые пересекаются под углом 120 градусов. Изучением многоугольников в целом и гексагона в частности занимался отец геометрии Евклид, который в «Началах» предложил способ построения правильного шестиугольника при помощи циркуля и линейки.
Вокруг любой правильной геометрической фигуры можно описать окружность или вписать ее внутрь. Гексагон не исключение. Сторона фигуры a и радиусы описанной окружности R и вписанной r соотносятся как:
Главная особенность гексагона состоит в том, что сторона многоугольника и радиус описанной окружности абсолютно равны, так как 2sin(pi/6) = 1.
Примеры шестиугольников
Гексагон — довольно распространенная геометрическая фигура. В человеческой повседневности форму шестиугольника принимают грани таких объектов как гайки, карандаши или детали машин. В природе шестиугольную форму имеют пчелиные соты, снежинки, а также кристаллические решетки некоторых соединений углерода. Кроме того, существует уникальное космическое явление на Сатурне — гигантский гексагон, который представляет собой атмосферный вихрь в виде правильного шестиугольника.
Шестиугольник — эффективная фигура, позволяющая замостить поверхность без пробелов или наложений. Кафель или тротуарная плитка часто принимают форму гексагона, однако наиболее выдающимся примером замощения поверхности шестиугольником является Мостовая гиганта — памятник природы, образованный соединением более 40 000 базальтовых колонн. Шестиугольные колонны Мостовой гиганта образовались в результате древнего извержения вулкана и элегантно замостили поверхность североирландского побережья.
Периметр гексагона
Периметр плоской фигуры — это числовая характеристика, показывающая сумму длин всех его сторон. Гексагон — правильная геометрическая фигура, следовательно, все ее стороны равны. Формула для вычисления периметра шестиугольника предельно проста:
Кроме того, благодаря замечательному свойству шестиугольника, периметр можно вычислить, зная радиус описанной окружности:
Наш калькулятор также использует зависимость между стороной гексагона и радиусом вписанной окружности, поэтому вы можете рассчитать периметр геометрической фигуры, зная только одну из трех переменных на выбор. Кроме того, калькулятор автоматически рассчитает не только периметр, но и остальные атрибуты шестиугольника. Рассмотрим пару примеров.
Примеры из реальной жизни
Снежинка
Снежинка представляет собой снежный или ледяной кристалл в форме правильной шестиугольной пластинки. Естественно, снежинка — слишком мала для того, чтобы мы могли измерить ее натуральный размер и посчитать периметр на онлайн-калькуляторе. Однако включим воображение и представим, что одна сторона снежинки имеет длину, равную 12 условных единиц. Для подсчета периметра такого кристалла нам понадобится просто умножить длину стороны на 6 или ввести значение в форму калькулятора «Сторона». Мы получим ответ:
Также мы узнали, что в нашу воображаемую снежинку мы можем вписать окружность с радиусом r = 10,39.
Школьная задача
В задаче по геометрии требуется найти периметр правильного шестиугольника, зная, что радиус вписанной в него окружности составляет 15 см. Мы знаем, что радиус окружности и сторона гексагона соотносятся как r = 0,866 a и можем вручную подсчитать сначала длину стороны, а затем периметр плоской фигуры. Мы можем сэкономить время и просто указать значение радиуса в ячейке калькулятора «Радиус вписанной окружности r» и получить мгновенный результат:
Заключение
Шестиугольник — эффективная фигура, которая встречается как в природе, так и в человеческой повседневности. Используйте наш онлайн-калькулятор для расчета периметра правильных шестиугольников.
Источник
Шестиугольник описанный около окружности формулы
Калькулятор для вычисления стороны правильного шестиугольника по известным данным.
При известном радиусе R описанной вокруг правильного шестиугольника окружности сторона a имеет такое же значение как и радиус R описанной вокруг шестиугольника окружности.
При известном радиусе r окружности вписанной в правильный шестиугольник сторона a вычисляется как отношение двух радиусов вписанной в правильный шестиугольник окружности и корня из числа 3.
Формула для вычисления стороны правильного шестиугольника при известном радиусе вписанной в правильный шестиугольник окружности:
r – радиус окружности вписанной в правильный шестиугольник,
a – сторона правильного шестиугольника.
При вводе данных дробную часть от целой, отделяйте точкой, а не запятой.
На данной странице калькулятор поможет рассчитать площадь правильного шестиугольника онлайн. Для расчета задайте длину стороны или радиус окружности.
Шестиугольник – многоугольник у которого все стороны равны, а все внутренние углы равны 120°.
Через сторону
Формула для нахождения площади правильного шестиугольника через сторону:
Через радиус описанной окружности
Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:
Определение длины стороны правильного многоугольника по радиусу вписанной окружности
От нашего нового пользователя поступил вот такой запрос:
«Калькулятор должен вычислять длину стороны правильного многоугольника (шестиугольник, пятигольник) по указанному диаметру (или радиусу) описанной окружности».
Удовлетворяем запрос оперативно. Заметим, что для решения задачи нужно найти длину третьей стороны треугольника, исходящего из центра описанной окружности и опирающегося на две соседние вершины правильного многоугольника. Про этот треугольник известно многое: длины двух сторон — это радиусы описанной окружности, и угол, как нетрудно заметить, — это 360, деленное на число вершин правильного многоугольника. Далее используется соотношение из теоремы синусов — две стороны относятся друг к другу также как и синусы противолежащих им углов. Поскольку треугольник равнобедренный и сумма углов в треугольнике равна 180 градусам, угол, противолежащий радиусу вычисляется тривиально. Результат — ниже.
Источник