Как найти больший угол равнобедренной трапеции если известны 2 угла
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.
Сумма углов треугольника АВС равна 180°, поэтому угол ABC равен 180° − 30° − 50° = 100°. Сумма противоположных углов равнобедренной трапеции равна 180°, поэтому 180° − 100° = 80°.
Сумма двух углов равнобедренной трапеции равна 140°. Найдите больший угол трапеции. Ответ дайте в градусах.
Так как сумма односторонних углов трапеции равна 180°, в условии говорится о сумме углов при основании. Поскольку трапеция является равнобедренной, углы при основании равны. Значит, каждый из них равен 70°. Сумма односторонних углов трапеции равна 180°, поэтому больший угол равен 180° − 70° = 110°.
Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:2. Ответ дайте в градусах.
Пусть x — меньший угол трапеции, а 2x — больший угол. У равнобедренной трапеции углы при основаниях равны, поэтому их сумма равна x + 2x + x + 2x = 6x. Поскольку она равна 360°, находим: х = 60°.
Основания трапеции равны 4 см и 10 см. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.
Так как KN — средняя линия трапеции, то KL и LN средние линии треугольников ABC и СAD соответственно.
,
Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
Сумма углов треугольника ACD равна 180°, поэтому . Так как основания трапеции параллельны, углы CAD и BCA равны как накрестлежащие. Так как трапеция равнобедренная, сумма её противоположных углов равна 180°, поэтому
.
Источник
Углы равнобедренной трапеции
Углы равнобедренной трапеции. Здравствуйте! В этой статье речь пойдёт о решении задач с трапецией. Данная группа заданий входит в состав экзамена, задачки простые. Будем вычислять углы трапеции, основания и высоты. Решение ряда задач сводится к решению прямоугольного треугольника, как говориться: куда мы без теоремы Пифагора, синуса и косинуса ?
Работать будем с равнобедренной трапецией. У неё равны боковые стороны и углы при основаниях. О трапеции есть статья на блоге, посмотрите.
Отметим небольшой и важный нюанс, который в процессе решения самих заданий подробно расписывать не будем. Посмотрите, если у нас дано два основания, то большее основание высотами, опущенными к нему, разбивается на три отрезка – один равен меньшему основанию (это противолежащие стороны прямоугольника), два других равны друг другу (это катеты равных прямоугольных треугольников):
Простой пример: дано два основания равнобедренной трапеции 25 и 65. Большее основание разбивается на отрезки следующим образом:
*И ещё! В задачах не введены буквенные обозначения. Это сделано умышленно, чтобы не перегружать решение алгебраическими изысками. Согласен, что это математически неграмотно, но цель донести суть. А обозначения вершин и прочих элементов вы всегда можете сделать сами и записать математически корректное решение.
27439. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.
Для того чтобы найти угол необходимо построить высоты. На эскизе обозначим данные в условии величины. Нижнее основание равно 65, высотами оно разбивается на отрезки 7, 51 и 7:
В прямоугольном треугольнике нам известна гипотенуза и катет, можем найти второй катет (высоту трапеции) и далее уже вычислить синус угла.
По теореме Пифагора указанный катет равен:
27440. Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен 5/7. Найдите боковую сторону.
Построим высоты и отметим данные в условии величины, нижнее основание разбивается на отрезки 15, 43 и 15:
27441. Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен (2√10)/7. Найдите меньшее основание.
Построим высоты. Для того чтобы найти меньшее основание нам необходимо найти чему равен отрезок являющийся катетом в прямоугольном треугольнике (обозначен синим):
Можем вычислить высоту трапеции, а затем найти катет:
По теореме Пифагора вычисляем катет:
Таким образом, меньшее основание равно:
27442. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен 5/11. Найдите высоту трапеции.
Построим высоты и отметим данные в условии величины. Нижнее основание разбивается на отрезки:
Что делать? Выражаем тангенс известного нам угла при основании в прямоугольном треугольнике:
27443. Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен 13/8. Найдите большее основание.
Строим высоты и вычисляем чему равен катет:
Таким образом большее основание будет равно:
27444. Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.
Строим высоты и отмечаем известные величины на эскизе. Нижнее основание разбивается на отрезки 35, 17, 35:
По определению тангенса:
77152. Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.
Построим эскиз, построим высоты и отметим известные величины, большее основание разбивается на отрезки 3, 6 и 3:
Выразим гипотенузу обозначенную как х через косинус:
Из основного тригонометрического тождества найдём cosα
27818. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 50 0 ? Ответ дайте в градусах.
Из курса геометрии нам известно, что если имеем две параллельные прямые и секущую, что сумма внутренних односторонних углов равна 180 0 . В нашем случае это
C условии сказано, что разность противолежащих углов равна 50 0 , то есть
Так как у равнобедренной трапеции углы при основании равны, то есть угол А равен углу В, то можем записать
Имеем два уравнения с двумя неизвестными, можем решить систему:
*Конечно, эту задачу можно было легко решить просто перебирая пары углов )
27833. В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними 60 0 . Найдите меньшее основание.
Построим высоты DE и CF:
Меньшее основание равно отрезку EF, так как DC и EF это противолежащие стороны прямоугольника. Отрезок EF мы можем найти если вычислим АЕ. Выразим этот катет прямоугольного треугольника ADE через функцию косинуса:
Так как AE=FB=5, то EF=25–5–5=15. Следовательно и DC=15.
27837. Основания равнобедренной трапеции равны 15 и 9, один из углов равен 45 0 . Найдите высоту трапеции.
Из точек D и C опустим две высоты:
Как уже сказано выше они разбивают большее основание на три отрезка: один равен меньшему основанию, два других равны друг другу.
В данном случае они равны 3, 9 и 3 (в сумме 15). Кроме того, отметим что высотами отсекаются прямоугольные треугольники, причём они являются равнобедренными, так как углы при основании равны по 45 0 . Отсюда следует, что высота трапеции будет равна 3.
Источник
Как найти больший угол трапеции
Здравствуйте!
Помогите решить!
Как найти больший угол трапеции, если трапеция равнобедренная, а два ее угла в сумме дают 98 градусов.
Спасибо!
Задача.
Как найти больший угол трапеции, если тр-ция равнобедренная, а два ее угла в сумме дают 98 градусов.
Решение.
В условии сказано, что тр-ция равнобедренная. Из этого следует, что при две пары ее углов при обоих осн-ниях будут равны.
Также о тр-ции известно, что сумма ее углов, которые прилегают к любой из боковых сторон, равна 180 град.
В условии задана сумма углов, которая меньше, чем 180 град. Следовательно, задана сумма углов, прилегающих к большему основанию, так как эти углы всегда острые, а их сумма, соответственно, будет меньше 180 град.
Из св-в равнобедренной тр-ции получаем, что каждый из углов при большем основании будет равен 98 / 2 = 49 град.
Найдем больший угол тр-ции:
180 – 49 = 131 град.
Это следует из св-в прилегающих к боковой стороне углов, рассмотренном выше.
Ответ. 131 град.
Можно было на этапе определения, что в условии задана сумма углов при большем основании воспользоваться св-вом углов любого четырехуг-ника, согласно которому сумма всех углов произвольного четырехуг-ника (в том числе и тр-ции) равна 360 град. Далее из этой суммы вычесть сумму двух равных острых углов:
360 – 98 = 262 град.
А поскольку тупые углы при меньшем основании равнобедренной тр-ции также равны, то полученное значение нужно разделить на 2:
262 / 2 = 131 градус.
Оба способа одинаково правильные и практически одинаково рациональные.
Источник
Найдите больший угол равнобедренной трапеции
Здравствуйте!
Помогите решить задачу:
Найдите больший угол равнобедренной трапеции, если известно, что большая диагональ образует с нижним основанием и боковой стороной углы по 30 и 45 градусов соответственно.
Спасибо!
Задача.
Найдите больший угол равнобедренной трапеции, если известно, что большая диагональ с нижним основанием и боковой стороной образует углы по 25 и 55 градусов соответственно.
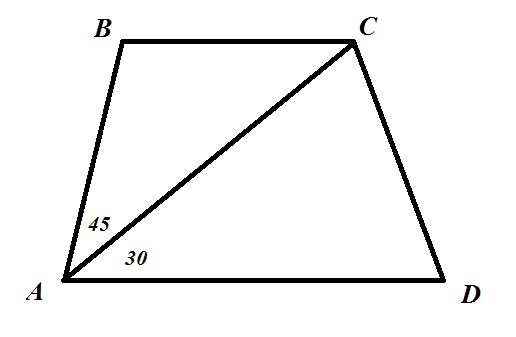
Решение.
Данную задачу можно решить двумя несколько отличающимися способами, которые, в принципе, равнозначны по сложности.
Рассмотрим первый способ.
Об углах любой трапеции известно, что сумма двух углов, которые прилегают к одной из сторон, равна 180 градусов. Исходя из этого, сумма углов, прилегающих к стороне АВ равна:
угол CAD + угол CAB + угол В = 180
25 + 55 + угол В = 180
угол В = 180 – 25 – 55
угол В = 100 градусов.
Таким образом, больший угол заданной равнобедренной трапеции равен 100 градусов.
Рассмотрим второй способ.
Из условия известно, что трапеция равнобедренная. Следовательно, углы при ее основаниях равны друг другу. То есть у основания AD угол А равен углу D, а у основания ВС угол В равен углу С.
Поскольку угол А = 55 + 25= 80 градусов, то и угол D = 80 градусов.
Также известно, что если сложить размеры всех углов в любом четырехугольнике, то получим 360 градусов. Запишем для данного случая:
угол А + угол В + угол С + угол D = 360
80 + 2 * угол В + 80 = 360
2 * угол В = 360 – 80 – 80
2 * угол В = 200
угол В = 100 градусов.
Источник
































